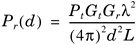Home Networking Basis: Transmission Environments and Wired/Wireless Protocols
| In an inside home environment, the field strength of a radio wave can be enhanced by reflections from surrounding walls and attenuated by barrier walls. These effects can be included by introducing a modification factor into the free space field strength expression. The modified field strength estimation formula is Equation 5.28
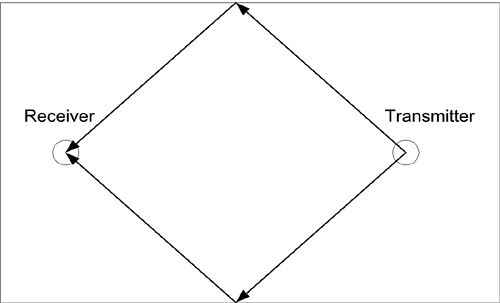
where L is the modification factor whose value could be smaller than one for the effect of reflection enhancement or larger than one for the effect of barrier attenuation. The amount of reflection enhancement can be estimated with knowledge of the room: the wall enclosure, room dimension, and locations of the transmitter and the receiver. For a simple illustration (Figure 5.9), we assume incident and reflection angles are all 45° for the floor, ceiling, and two side walls. At that angle, strengths of the first reflected wave are 0.14 and 0.37 for parallel and perpendicular components, respectively. Summarizing all reflected energies from four interfaces together, strengths of the first reflected wave are 0.56 and 1.48 for parallel and perpendicular components, respectively. However, at 45°, the travel distance of the reflected wave is Figure 5.9. A Top View of a Room with a Transmitter and a Receiver
Also at 45°, strengths of the transmitted wave are 0.85 x 0.9 = 0.756 and 0.62 x 0.6 = 0.372 for parallel and perpendicular components, respectively. Therefore, the value of L can be between 1 and 3 to account for the effect of wall attenuation. For a room dimension of 16 ft by 22 ft, a ceiling height of 8 ft, and a distance of 3 ft from the transmitter or the receiver to the nearby end wall, the strength is estimated as follows. For the two end walls, the energy reflection coefficient is 0.25 and the distance factor is (16/22)2. The total strength due to two end wall reflections is 0.25 x (16/22)2 x 2= 0.264. For the two side walls, the energy reflection coefficients are 0.14 and 0.37 for parallel and perpendicular components, respectively. The distance factor is Figure 5.10 shows received power to transmit power ratios according to the modified field strength formula with L = 0.5, 1, and 3 for the 900-MHz frequency band. The top curve corresponds to L = 0.5 with reflection enhancement. The middle one corresponds to L = 1 (i.e., the free space formula). The bottom one corresponds to L = 3 representing additional losses due to wall barriers. Figure 5.10. Received Power to Transmit Power Ratio at 900 MHz
Figure 5.11 shows received power to transmit power ratios also according to the modified field strength formula for the 2.4-GHz frequency band. The top (L = 0.5), middle (L = 1), and bottom (L = 3) curves are plotted together with some real indoor signal strength measurements. These measurements are close to estimations according to the formula. At longer distances, the radio wave is usually attenuated by multiple wall barriers resulting in heavier losses. Figure 5.11. Received Power to Transmit Power Ratio at 2.4 GHz with Measurements
Figure 5.12 shows top (L = 0.5), middle (L = 1), and bottom (L = 3) curves together with some other real indoor signal strength measurements for the 5.7-GHz frequency band. These measurements are also close to estimations according to the formula. Figure 5.12. 5.7 GHz with Measurements
Within the same frequency band and with fixed antenna gains, the power loss defined as the received power to transmit power ratio expressed in decibels is proportional to the log value of the distance.
To fit general measurements, the power loss model is expressed as Equation 5.29
where n is usually between 2 and 5. |