Six Sigma Fundamentals: A Complete Introduction to the System, Methods, and Tools
|
SPC really addresses three distinct items—statistics, process and control. To appreciate the essence of SPC, one must think of employing the language of statistics, focused on a process for the purpose of control. An overview of what each aspect contributes to the total concept will prove helpful, but it is important to note that SPC is really a methodology to study the behavior of the process rather than to control anything.
Statistics. Statistics has frequently been described in a broad sense as a universal language, which is most useful in describing physical variability. Any group of data or numbers can be described and analyzed through statistical methods. Effective use of the language is enhanced by choosing the most pertinent data and handling it in the most efficient manner to best describe the physical variability of interest.
A familiar analogy involves engineering drawing as a universal language employed to describe the physical shape of a product, for example, a blueprint. In an analogous sense, a control chart (a central tool of SPC) is a document utilizing statistics as a universal language to describe the physical variability of a process.
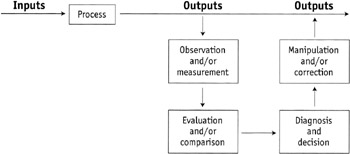
Process. A process may be defined as a combination of inputs, both durable and convertible resources, for the purpose of obtaining desired quality outputs. The transformation (value added) of the inputs into the outputs is the process. Figure 4.1 shows such a process.

The convertible resources are the inputs: materials, energy and information. Traditionally speaking, they have been called manpower, machine, material, method, measurement and environment. Output, on the other hand, indicates products, information and services. The transformation itself may be part of the durable resources or a combination of the durable as well as the convertible resources including environment.
Using this definition, a process may be thought of in global terms as collectively all the operations of a business, or in a much more narrow sense as a particular operation of a specific machine. Both views are appropriate. Typically, opportunities for improvement are illuminated by removing as much of the noise as possible by narrowing the focus to smaller elements of the total process.
Control. Control, the final word of SPC, is frequently misconstrued as a misnomer. The question arises, Does SPC control anything? Strictly speaking, it does not. However, control is not only an appropriate term, but also the key to the successful implementation of SPC. The classical control cycle consists of at least four actions: observing or measuring, comparing, diagnosing and correcting. Any time these four actions are successfully accomplished, a control cycle may be applied to many different systems in various ways.
Organizational improvement strategies can be condensed into two generic applications of such a control cycle: product control and process control. Successful completion in either case may lead to improvement. However, improvement is significantly better through process control.
Process control versus product control
The distinction between process control and product control is depicted in Figure 4.2. Product control orients the classical control cycle in a feed-forward [in time] mode. Process control is oriented towards a backward mode emphasizing the process.
The major differences between the two approaches are summarized in Table 4.2.
| PRODUCT CONTROL | PROCESS CONTROL | |
|---|---|---|
| Focus | PRODUCT | PROCESS |
| Goal | Variability within specification limits | On target with smallest variation |
| Typical Tools | Acceptance sampling plans | Control charts |
| Improvement Nature | Outgoing quality only | Quality plus productivity |
| Philosophy | Detection and containment of problematic occurrences | Prevention of problematic occurrences |
SPC strategy
To pursue an SPC strategy, one must first understand the process, and to gain that understanding one must first have knowledge of the process. The knowledge is generated through the definition, collection and analysis of data. Without data, nothing will happen.
The first step of the process control strategy involves the definition of the data—that is, the operational definition of what is to come. The second is the actual collection of data. Careful thought about how to obtain the most pertinent data should precede data gathering. The data should be collected accurately and precisely to maximize the information richness with respect to the process.
Measurements of one set of components are listed below. The components were all measured at the same location with the same measuring instrument by the same person.
| .0138 | .0150 | .0164 | .0132 | .0119 | .0144 | .0144 | .0140 |
| .0146 | .0158 | .0140 | .0125 | .0147 | .0149 | .0163 | .0135 |
| .0161 | .0138 | .0126 | .0147 | .0153 | .0157 | .0154 | .0150 |
| .068 | .0173 | .0142 | .0148 | .0142 | .0136 | .0165 | .0145 |
| .0146 | .0135 | .0145 | .0176 | .0156 | .0152 | .0135 | .0128 |
Since it is difficult to see how the data arises in a frequency sense, a more meaningful presentation of the data is desired. A simple raw tally sheet might be constructed where each x represents a frequency of one measurement: (The data have been coded as whole numbers.)
While it is helpful to unscramble the numbers and present them graphically, the question for the simple raw tally sheet presentation is, "How information rich is it?" A more informed view may be obtained through several steps for grouping the data into class intervals and presenting the data as a "frequency histogram," a "frequency polygon," or a "frequency curve." The following steps are useful in grouping the data into a frequency distribution for presentation in any of these three pictures. The actual use of each is dependent upon the preference of the experimenter and whether or not he or she is interested in the individual representation or the shape of the distribution.
-
Count the number of measurements or observations (N).
-
Determine the number of class intervals (K) (see Table 4.3).
Table 4.3: Guide for determining the number of class intervals NUMBER OF OBSERVATIONS
NUMBER OF CLASS INTERVALS
(N)
(K)
30–50
5–7
51–100
6–10
101–250
7–12
Over 250
10–20
-
Determine the data range (R). R = Highest value minus lowest value.
-
Divide the data range by the number of class intervals to obtain an estimated class size (R/K).
-
Round estimated class size to a convenient number.
-
Determine class boundaries.
-
Determine one-half number accuracy.
-
Adjust class boundaries.
-
Tabulate data.
For our example, the frequency distribution for group data is shown as:
| 138 | 150 | 164 | 132 | 119 | 144 | 144 | 140 |
| 146 | 158 | 140 | 125 | 147 | 149 | 163 | 135 |
| 161 | 138 | 126 | 147 | 153 | 157 | 154 | 150 |
| 168 | 173 | 142 | 148 | 142 | 136 | 165 | 145 |
| 146 | 135 | 145 | 176 | 156 | 152 | 135 | 128 |
-
N = 40
-
K = 5 to 7
-
R = 176 - 119 = 57
-
R/K = 57 / 7 = 8.14
-
9
-
117, 126, 135, 144, 153, 162, 171, 180
-
.5
-
117.5, 126.5, 135.5, 144.5, 153.5, 162.5, 171.5, 180.5
-
… …
| THICKNESS X | TALLY | FREQUENCY f |
|---|---|---|
| | ||
| 117.5-126.5 | /// | 3 |
| 126.5–135.5 | ///// | 5 |
| 135.5–144.5 | ///////// | 9 |
| 144.5–153.5 | //////////// | 12 |
| 153.5–162.5 | ///// | 5 |
| 162.5–171.5 | //// | 4 |
| 171.5–180.5 | // | 2 |
Frequency histogram
A frequency histogram or histogram is a special type of column graph consisting of a set of rectangles where:
-
The bases are on a horizontal axis (x-axis) with centers at the class marks.
-
The width of the rectangles represents the class size.
-
The height of the rectangles reflects the respective class frequency.
And consequently,
-
The areas of the rectangles are proportional to the class frequencies. The following is a visual representation:
Label either class marks (more common) or class boundaries on the horizontal axis.
Interpretation
Each of the foregoing steps to group data distribution will generate graphs of the data to clarify the data and to provide a clear picture. The interest should center upon how the data illuminates the process. With some additional information the experimenter can calculate the capability of the process, the amount of rejects and the statistical confidence of the data. For example, the desired target value may be calculated—in this case, it is 150; the desired boundary may be worked out—in this case, any component measuring greater than 195 will be cost prohibitive; and we can calculate the capability—in this case, any component measuring less than 105 will not be functional.
How should one assess process behavior?
Fundamentally there are two ways of looking at data: by measuring or by observing. With each one there are two approaches for analysis: compress the data into an instant of time, thereby creating a frequency plot, or view how data arises over time, thereby creating a control chart. An experienced experimenter should know how to maximize the information by using the appropriate tools and techniques. In either case, the objective is to understand variation. Variation is the difference between each piece. However, collectively each piece variation contributes to a set pattern, which is called a distribution. This distribution may differ depending on location, spread, shape or in any combination.
Behavior of the process
Process control charts. As discussed, the idea of understanding the process is a function of a specific strategy. The strategy is to monitor the process through a control chart or evaluate the product through a frequency curve. Both are acceptable; however, there is more information to be gained with the control chart.
Underlying the control chart is the concept that variability can be separated into two arenas with respect to nature or source. Distinguishing the unstable variability from inherent or stable variability of the process is the role of the control chart, the product of statistical thinking and the foundation from which potential quality improvement stems.
The control chart is a graphic portrayal of how data of interest arises over time. Special causes of variability (process instabilities) arise or evolve in unusual manners. Distinguishing such a source of variability (special cause) from the stable variability (common causes) is possible by identifying unusual patterns and unexpected data points on the control chart.
The control chart concept is consistent for the various quantities of interest from the output. Awareness of the reference distribution underlying a particular control chart (depending upon the quantity being plotted) is paramount. A graphical representation of a control chart for sample averages (Xs) is depicted in Figure 4.3.
While certainly not the only statistically based tool in the quest for never-ending quality improvement, the control chart provides a clear documentation of process variation in a form that guides appropriate diagnostic actions. As reduction of variability occurs, the same variability is witnessed by the data on the control charts. As variability is reduced, less masking of the smaller effects of improvements results and verification of even subtle and small improvements provides further benefits.
The main applications of control charts are:
-
To monitor process performance over time.
-
To aid in the quest for process improvement by verifying the authenticity of improvement actions.
-
To establish the basis for true process capability assessment.
Many types of control charts exist, and choosing the most efficient and appropriate chart for a particular characteristic of interest is paramount. Two general classifications of control chart types are:
-
Variable control charts.
-
Attribute control charts.
Variable charts should be employed when data from a continuous scale (measurements) are of interest. Attribute charts are used when discrete data are of interest. In general, the attribute data are countable data pertaining either to the number of non-conformities (defects) or non-conforming units (defectives).
A more complete control chart selection matrix has been provided in Figure 4.4. While this matrix does not include all possible types and variations of control charts, those in current major use in industry have been included.
Process variation. The purpose of a control chart is to view the behavior of the process over time. However, we can also view the behavior of a process in specific time with a histogram. That behavior may be due to either common or special causes. In either case, improvement in quality (reduction in variation) of the output may come as a result of either removing or reducing either or both types of causes.
Special cause. A source of variation that influences some (or all) of the measurements, but in different ways. (If special causes of variation are present, the output of a process will not be stable over time and cannot be predicted!) Therefore, special causes can be characterized as assignable, chaotic and unnatural.
Common cause. A source of variation that influences all of the measurements in the same way. (If only common causes of variation are present, the output of a process forms a distribution pattern that is stable over time and that pattern can be predicted!) Therefore common causes can be thought of as chance, random and natural.
What is the problem with variation? Variation is waste. Therefore, as variation increases so does the waste. Consequently, when one wants to determine, from the variability pattern in the data, which deviations from the target have been produced by special causes and which have been produced by just the common causes, they are interested in identifying the source of waste. Why is this important? Because the responsibility for corrective actions rests with different authority levels. Special causes frequently can be corrected at the process by the operator or the supervisor at the local level. On the other hand, common causes represent a system fault, which requires the attention of management to improve the process as necessary.
How can this be done? Has all the data come from the same process? The answer is to apply appropriate and applicable statistical techniques that have the ability to separate the presence of special causes in light of the ever present common causes. When this is done, improvement is the result. A pictorial representation of the process is shown in Figure 4.5. Table 4.4 represents some of the typical characteristics of variation.
| COMMON CAUSE | SPECIAL CAUSE | |
|---|---|---|
| Scope of Influence | All data in similar manner | Some (or all) data in dissimilar manner |
| Typical Identity | Many small sources | One or a few major sources |
| Nature | Stable and collective pattern is predictable. It is what is inherent or natural to the process | Sporadic irregular Unpredictable Appears & disappears |
| Improvement Action | Reduce common cause(s) Variability | Incorporate or eliminate |
| Improvement Responsibilty | SYSTEM fault Management | LOCAL fault Operator/supervisor |
Steps and phases of implementation
The objectives of any statistical process control program must be to:
-
Decrease quality costs by reducing scrap, rework and inspection costs by controlling the processes.
-
Decrease operating costs by optimizing the frequency of process adjustments and changes.
-
Improve productivity by identifying and eliminating the special causes.
-
Reduce variability and establish a predictable and consistent level of quality.
-
Increase customer satisfaction by reducing production variability, thereby producing a more trouble-free product.
-
Eliminate the dependence on mass inspection to achieve quality. Build the quality into the product or service.
-
Provoke process thinking among all levels of the organization.
For these items to be successful in any organization, they must be assessed, planned, supported and monitored through:
-
An official organization for SPC.
-
Training.
-
Implementation.
-
A philosophy of statistical and problem-solving techniques.
It is extremely important to recognize that the paths of product versus process control are quite different and they demand different approaches. In either case, a natural evolution of the need for the tools is paramount and we must never forget or become complacent about it.
So important is this natural evolution that one must understand that each input/process/output has its own level of involvement. This can be seen in Figure 4.6.
The process of involvement is done through at least the following activities:
Identify the team
Identify team members and titles
Identify area
Identify the initiation date
Identify the problem
Identify initial situation
Identify the objectives
Identify the analysis of the problem(s)
Identify the actions and resolutions including:
-
Date initiated
-
Description
-
Responsible persons
-
Date completed
Identify appropriate and applicable graphical presentations of results.
Identify appropriate and applicable permanent consolidation of results.
On the other hand, the control charting process is carried out through ten steps, which are:
-
Identify area of study.
-
Operationally define quality characteristics.
-
Assess measurement or observation system.
-
List potential special causes.
-
Determine sampling procedure size, frequency, by whom, etc.
-
Carefully record sample data by documenting important processes and noting conditions at the time the samples are drawn.
-
Continue charting to monitor process.
-
Analyze charts.
-
Reduce variability sources: special causes; common causes.
-
Plot charts.
Initiating control charts—variable data (pursuit of common cause characterization)
The following is a list of important considerations to keep in mind when initiating control charts when using variable data—that is, when attempting to characterize common cause variations.
-
Collect at least 25 samples prior to calculation of trial control limits.
-
Attain stability of the R chart prior to addressing the X-bar chart.
-
Remove sample values and revise limits if and only if special causes are identified.
-
Extend control limits as the process model only after statistical control has been established.
-
Establish stability (statistical control) prior to assessment of process capability.
Remember: The following guidelines are essential to keep in mind when initiating control charts.
-
The control limits at any given time should be the best estimate of common cause variability of the process.
-
The default position should generally be a sample size of five, taken once an hour. This typically works well as an initial plan.
-
At least 25 samples across at least a week should provide an initial characterization of the common cause variability for most processes.
Management responsibilities
The purpose of SPC in problem-solving and process control is to continually improve quality, productivity and costs. Management plays a key part in achieving this continual improvement. In this regard, an SPC initiative must have:
-
Top management commitment.
-
Top management involvement.
-
Team approach to problem identification and solving.
-
Statistical training at all levels.
-
Implementation of plans with supportive resources.
Perhaps the most important requirement in any organization embarking on an improvement initiative is the organization itself. That means its culture, attitude and approach are items of concern. The reason for this is that a total SPC approach stresses statistical thinking as a management tool, but combines that with substantive knowledge of the processes to yield improvement results. A coordinated effort to identify and to appropriately act upon sources of variability is paramount. Proper organization is the starting point; while a number of scenarios might accomplish the objectives, a model that has performed well in various industries is discussed in the following sections.
Establish a steering committee. This group has the authority to designate and oversee SPC efforts. Setting the structure for efficient closure of the process control loop should be an aggressive goal. This group should be active in setting goals, monitoring progress and ensuring that efforts are directed in a useful manner and that the various SPC efforts of different departments or groups are compatible.
Specific responsibilities are to:
-
Determine which areas should be addressed.
-
Ensure smooth movement of implementation.
-
Facilitate momentum-building by ensuring timely and appropriate follow-up action to requests.
-
Involve each stakeholder in specific tasks following the reports.
-
Recognize accomplishments.
Organize process teams. Teams integrated vertically around the processes, due to their levels of authority, work most efficiently. Collection and analysis of data, conducting of experiments and the pursuit of improvement for a particular process are all responsibilities of these groups. Specific initial responsibilities are:
-
Planning the process control charts, proper type and logistics appropriate and applicable.
-
Installing the control charts, training and providing suitable materials and routines for the production personnel.
-
Monitoring the process control data collection and process information gathering to ensure smooth and effective use of the tools.
-
Acting upon instabilities (irregularities of any kind in the team environment) and making sure that these instabilities are diffused and the team progresses as planned.
-
Monitoring and reporting progress, inhibitors, etc.
Institute an educational phase. The knowledge that is needed to improve any process has to be learned. Therefore, the goals of this step are to:
-
Familiarize the teams with the SPC, the cultural language of the organization, the jargon for the problem at hand and any other communication initiative that is required for the participants to function appropriately and effectively.
-
Provide the teams with some basic knowledge. Problem solving techniques, seven quality tools, and team dynamics are some examples.
-
Provoke thinking on an individual basis as to how this new knowledge fits into daily work.
-
Provoke thinking of possible positive, as well as negative, implications of this new knowledge on a system basis.
The prerequisites for this knowledge are:
-
Management awareness and understanding of the basic SPC philosophy.
-
Commitment of resources.
-
Organization for implementation.
Use the knowledge. The fourth step of the model is the utilization phase. The knowledge that has been learned has been (or is in the process of being) implemented. There are two stages to this phase of the model: the pilot application stage and the mature utilization stage.
The goals of the pilot application stage are to:
-
Build technical confidence and maturity in the critical mass (the amount of people that the organization needs for change to occur) that is responsible for implementation.
-
Demonstrate utility of the techniques to the teams.
-
Bring more structure or order to problem-solving.
The goals of the mature utilization stage are to:
-
Bring statistical/process thinking on board with new products and processes.
-
Solve the major problems based on your criteria of importance during the definition stage.
-
Realize the major gains.
-
Integrate improvement programs with existing programs or with the organization's objectives.
-
Transfer ownership to the system as a whole the process owner(s).
Institutionalize the knowledge. The final step is the institutionalization phase. At this stage, what has been learned must become part of the organizational culture, and this must be done as an automatic response. It creates the new status quo for improvement. Specifically, institutionalization means:
-
Gathering data, charting, analysis and taking action based on that data and analysis are now a daily discipline.
-
Relying on facts and statistical data are natural reactions.
-
Everyone speaks the common language of SPC.
-
SPC is an integral part of conducting business.
-
Everyone applies process control thinking in his or her job every day.
-
Statistical process control is perpetual because the benefits are recognized by all.
While some elements that need to be in place before an organization moves into this phase can be (and have been) enumerated, the timing of this phase is difficult to assess. With a clear vision of where the organization is headed, efforts for attaining the goal can be better directed.
Whereas SPC is an important element in the six sigma endeavor, the following problems associated with it are not uncommon:
-
Misunderstanding the concepts of process control versus product control as they relate to both quality and productivity.
-
A misconception of the physical difference between special and common causes as they relate to process performance.
-
A lack of understanding of what control charts are telling an operator versus what they are telling management.
-
An absence of a framework and methodology that rigorously identifies where statistical charting can best be employed for the most pertinent process diagnostic information.
-
A failure to accept the absolute importance of closing the process control loop, diagnosing root causes, following through with appropriate countermeasures and solidifying the improvement gains.
-
A lack of understanding of loss function. Use of the loss function concept serves as a means to evaluate quality in terms of loss due to variation in function on economic grounds, to articulate the economic interpretation of a specification limit and to assess the economic performance of a process.
Statistics used in control charting
This section provides the professional practitioner with some simple approaches to statistical understanding for the every-day application of some common charts, rather than an extensive litany of statistical tools. The section addresses computing an average, control limits for X and R charts, control limits for p charts, general formulae, capability, control chart construction guides for variable data and for attribute data and testing for normality and exponentiality. Also, some instructions for calculator usage is addressed.
Computing an average. There is a formula for computing averages. Knowing this formula is useful because it follows a pattern you will see in other statistics formulas. Here is what it looks like:
This is what the terms mean:
-
-
Σ is the summation sign. This symbol means you need to find the sum (total) of the numbers. Σ is always followed by a letter or letters to let you know which numbers to sum up.
-
Σ X is the symbol indicating the total sum of what you are trying to measure.
-
n is the symbol for how many numbers you added to get the Σ X total.
If you can remember this formula, you will have an easier time using your calculator.
An average alone does not tell you anything about the data used to find it. The two methods SPC uses to show how the average relates to the data are range and standard deviation.
Range is the difference between the highest and lowest values of data used for the average. The abbreviation for range is R. The formula for finding the range is:
R = Highest - Lowest
Standard deviation is a statistical unit of measure computed from all the data used for the average. There are two abbreviations for standard deviation: s and σ.
-
s is the standard deviation used when you use samples from a production run. This is called the sample standard deviation.
-
σ is the standard deviation used when you use an entire production run. This is called the population standard deviation.
Although standard deviations can be computed through longhand, it is easier to use a calculator.
For example, some calculators have statistics programs built into them. Once you learn to use this feature, you will appreciate how the calculator does number crunching for you. Calculators are not all the same. This example is based on Sharp EL-509S.
Getting into STAT mode:
-
Look above the ON key. STAT is outlined in brown. Anything in brown means you have to press the second function key first. (Every calculator has a key that is a different color and it has "2nd" printed on it. That is the second function key. It implies that the user must use this key before entering the function of choice to be calculated. When the second function key is activated, the functions shown in yellow are enabled.) To use STAT mode, press the second function key and then the ON key.
-
You should see STAT above the zero on your screen. Your calculator is now a statistics computer and a calculator. Make sure you use the keys identified in blue.
-
Find the three memory keys outlined in blue, and the gray key just above them. These are the four statistics keys. The top three statistics keys give you answers. The bottom statistics key enters data into the computer.
-
DATA key M+
This is the bottom statistics key. Numbers used to compute averages, totals, and standard deviations are called data. After you punch in a piece of data, pressing the DATA key by itself enters it into the STAT program.
-
Standard deviation key RM
This key can give you the two different standard deviations. Pressing it by itself will give you the sample standard deviation (abbreviated as s). s is the calculation you want when you deal with samples from an entire production run.
Pressing the second function key will give you the population standard deviation (abbreviated as σ). σ is the calculation you want when you deal with an entire production run.
-
Average key X ➡ M
Pressing this key by itself will give you the average (also known as X-bar or X) of the numbers in the STAT program.
-
Total key )
Pressing this key by itself will tell you how many numbers are in the STAT program (abbreviated n). This helps you keep track of where you are as you enter data.
To get the total (abbreviated Σx), you have to press the second function key and then press the key with the dot.
See how Σx is written in brown ink? Remember—brown ink always means you have to press the second function key first.
| IMPORTANT: | When you have completed the calculations for one set of data, you must clear out the old data before punching in new data. If you don't, the calculator will add the new data to the old data. |
The easiest way to clear out old data is to turn the calculator off, turn it back on and get back into STAT mode.
If you happen to make a mistake using STAT mode, it is best to start again by clearing out the bad data.
-
Advanced STAT Mode
If you have data from a frequency distribution chart, you can use a shortcut method of entering data. Like all shortcuts, you have to be careful when you use it.
Frequency distributions tell you how often a certain value comes up in your data. To enter this data into the STAT program:
-
Punch in the value.
-
Press the multiply key.
-
Punch in the frequency.
-
Press the data key.
Make sure n (how many numbers are in your STAT program) on your screen is the same as n from your data.
Control limits for X and R charts. Sometimes you will see this control limits formula:
This is really two formulas in one. Here is what the different parts mean:
-
-
-
is a math symbol that means add and subtract. Whenever you see this sign, it means there are two equations to solve. Do not confuse it with the + / - key on your calculator.
-
A2 is an SPC factor you get from a table on your charts. The number you use depends on your sample size. For instance, if your sample size is 5, A2 will always be 0.577.
-
Since the sign means there are two equations to solve, break this formula down. The two equations look like this:
-
-
To find control limits, you need values for
For this example, the sample size is 5,
| Step 1 | Write down both formulas. |
| Step 2 | Substitute values (numbers) for variables (letters). |
| Step 3 | Complete the multiplication. |
| Step 4 | Complete the addition and subtraction. |
| Step 5 | Round off the answers as needed. |
With your calculator, you can find both control limits without a great deal of extra writing. There are eight steps to follow. You have to be careful in following them, but once you get into the practice of it, you will be able to calculate these control limits with speed, accuracy, and confidence.
Because A2 and
To find the upper control limit, add the value for
The eight steps to find the control limits using the calculator are:
| STEPS | KEYSTROKES |
|---|---|
| Step 1. Multiply the value of A2 times the value of | |
| Step 2. Put the answer in memory. | |
| Step 3. Add | |
| Step 4. Round off your answer for the upper control limit. | |
| Step 5. Subtract the memory. | |
| Step 6. Check the answer. If the answer is the same as | |
| Step 7. Hit the equals key again. This will subtract the memory. | |
| Step 8. Round off the answer for the lower control limit. |
Control limits for p charts. Sometimes you will see the control limits formula like this:
This means the control limits for p charts are three standard deviations both sides of the average.
Just like the control limits formula for the X-bar charts, it is really two formulas in one. And once you know what the individual parts mean, you will know what the formula means. Here is what the parts mean:
-
CLp is "The control limits for p." This an abbreviation for the upper and lower control limits for p charts.
-
p is the average proportion defective. A proportion is the decimal answer to a fraction. This is read "pbar".
-
is a math symbol that means add and subtract. Whenever you see this sign, it means there are two equations to solve. Do not confuse it with the + / - key on your calculator.
-
√ is a math sign meaning the square root. There is a key for this on the calculator.
-
n is the sample size.
-
If you know what pbar is, this formula is seven different math problems—nine if you include rounding.
Since there are always two control limits, the first thing to do is break the formula down into the upper control limit formula and the lower control limit formula.
The upper control limit formula looks like this:
This is an addition problem. It tells us that the upper control limit on a p chart is the average plus three standard deviations.
The lower control limit formula looks like this:
This is a subtraction problem. It tells us that the upper control limit on a p chart is the average minus three standard deviations.
The trick is to find the three standard deviations. That is five math problems right there—two multiplication, one square root, a division, and a subtraction. Ground rules in math tell you in what order to solve the problems. Once you find the three standard deviations, you can find both control limits. To master the trick:
-
Find the answer to 1 minus pbar.
-
Multiply by pbar.
-
Divide by n.
-
Find the square root.
-
Multiply by three.
Now you have the values of three standard deviations. Add this number to pbar for the upper limit. Subtract this number from pbar for the lower limit. Both limits should be rounded off to the same number of decimal places as pbar.
With the help of your calculator, you can work out these control limits.
The calculator instructions for control limits are:
| STEPS | KEYSTROKES |
|---|---|
| Step 1. Put pbar in memory. | |
| Step 2. Find one minus pbar. | |
| Step 3. Multiply by pbar. | |
| Step 4. Divide by n. | |
| Step 5. Find the square root. | |
| Step 6. Multiply by three. | |
| Step 7. Put the answer in memory. | |
| Step 8. Add pbar. | |
| Step 9. Round off the answer for the upper control limit. | |
| Step 10. Subtract the memory. | |
| Step 11. Check the answer against pbar. If the answer and pbar are the same, go to step 11. If the answers are different, you will have to start again. | |
| Step 12. Hit the equals key again. | |
| Step 13. Round off answer to give you the lower control limit. |
General formulas. The following general formulas are useful in SPC.
-
Arithmetic mean (average) from ungrouped data.
| For a population: | |
| For a sample: | |
| For the average of the average | |
where ΣX is the sum of all observed population (or sample) values. N is the number of observations in the population and n is the number of observations in the sample. The Σ
-
Arithmetic mean (average) from grouped data.
| For a population: | |
| For a sample: | |
Where fX is the sum of all class-frequency (f) times class-midpoint (X) products. N is the number of observations in the population, and n is the number of observations in the sample.
-
Median from ungrouped data.
| For a population: | |
| For a sample: | |
Where X is an observed population (or sample) value, N is the number of observations in the population, and n is the number of observations in the sample.
-
Median from grouped data.
| For a population: | |
| For a sample: | |
Where L is the lower limit of the median class, f is its absolute frequency, and w is its width, while F is the sum of frequencies up to (but not including) the median class, N is the number of observations in the population and n is the number of observations in the sample.
-
Mode from grouped data.
| For a population or a sample: | |
Where L is the lower limit of the modal class, w is its width, and d1 and d2, respectively, are the differences between the modal class frequency density and that of the preceding or following class.
-
Weighted mean from ungrouped data.
| For a population: | |
| For a sample: | |
Where Σw1X is the sum of all weight (w) times observed-value (x) products, while w equals N (the number of observations in the population) or n (the number of observations in the sample).
-
Mean absolute deviation
From ungrouped data
| For population: | |
| For a sample: | |
Where Σ|X - μ| is the sum of the absolute differences between each observed population value, X, and the population mean, μ, while N is the number of observations in the population, and where Σ|X -
From grouped data:
Denoting absolute class frequencies by f and class midpoints by X, substitute Σf|X - μ| or Σf|X -
-
Variance from ungrouped data.
| For a population: | |
| For a sample: | |
Where Σ(x - μ)2 is the sum of squared deviations between each population value, X, and the population mean, μ, with N being the number of observations in the population, while Σ(x -
-
Variance from grouped data.
| For a population: | |
| For a sample: | |
Where absolute class frequencies are denoted by f, class midpoints of grouped population (or sample) values by x, the population (or sample) mean by μ (or
-
Standard deviation from ungrouped data.
| For a population: | |
| For a sample: | |
Where Σ(x - μ)2 is the sum of squared deviations between each population value, x, and the population mean, μ with N being the number of observations in the population, while Σ(x -
-
Standard deviation from grouped data.
| For a population: | |
| For a sample: | |
Where absolute class frequencies are denoted by f, class midpoints of grouped population (or sample) values by x, the population (or sample) mean by μ (or
-
Variance from ungrouped data—shortcut method.
| For a population: | |
| For a sample: | |
Where Σx2 is the sum of squared population (or sample) values, μ2 is the squared population mean and
-
Variance from grouped data—shortcut method.
| For a population: | |
| For a sample: | |
Where Σfx2 is the sum of absolute-class-frequency (f) times squared-class-midpoint (x) products, μ2 is the squared population mean and
Capability. There are four aspects of capability: process capability, capability ratio, capability index and target ratio percent. Each is outlined here.
-
Process capability
Where USL and LSL are the upper and lower specifications and σx is the standard deviation.
-
Capability ratio
Where USL and LSL are the upper and lower specifications and σx is the standard deviation.
-
Capability index
Where Zmin is the less value of (USL-Xbar)/3σ and (Xbar-LSL)/3σ
-
Target ratio percent
| Special note: | Capability in six sigma is a very important issue. Therefore, even though the above formulas are the generic ones, the practitioner for the six sigma project should be aware of the following conditions: |
For variable data: we use the Cp or Cpk for short-term capability and for long capability we use the Pp or Ppk. The difference between the two is the calculation of the sigma in the denominator of the formula. That is for Cpk we use σ =
For attribute data, we use the ppm, DPU, or the DPM value.
The universal metric for capability has been the sigma value. However, more and more companies are reporting the actual Z value without discriminating for short or long capability.
Control chart construction guide for variable data. This is shown in Table 4.5.
| QUANTITY | CENTRAL LINE | UPPER CONTROL LIMIT | LOWER CONTROL LIMIT | SAMPLE | NOTES |
|---|---|---|---|---|---|
| Statistic | Average | UCL | LCL | n | Generic form |
| Average 3 σ statistic | |||||
| Sample average | | | | Small: Prefer n < 10 typ: n = 5 | Normal distribution w/R chart |
| R: Range | | | | Same (above) | Analyze 1st |
| Sample average | | | | 7< n < 25 | Normal distribution w/S chart |
| Std. Dev | | | | Same (above) | Analyze 1st |
| X Individual values | | | | n = 1 | Normality assumed < Sensitive |
| Rm Moving range | | | | Small usually n = 2 | Correlated w/X chart |
| Median X | | | | typ: n = 5 | < Sensitive |
| Range | | | | Same (above) | Analyze 1st |
Control chart construction guide for attribute data. This is shown in Table 4.6.
| QUANTITY | CENTRAL LINE | UPPER CONTROL LIMIT | LOWER CONTROL LIMIT | SAMPLE | NOTES |
|---|---|---|---|---|---|
| Statistic | Average | UCL | LCL | n | Generic form |
| Average ア 3 σ statistic | |||||
| p Proportion defective | | | | Prefer | Binomial distribution LCL < 0 = >0 |
| np Number of defectives | | | | Prefer | Binomial distribution LCL < 0 = >0 |
| Standardized | O | +3 | -3 | Variable | Standardize p: Stabilize UCL & LCL |
| C Number of defects per inspection unit | | | | Prefer | Poisson distribution Expected # small: great opportunity |
| U Number of defects per inspection unit | | | | Prefer | Poisson distribution Expected # small: great opportunity |
Testing for Normality and Exponentiality. Table 4.7 demonstrates this test.
| CONDITION | TEST FOR NORMALITY | TEST FOR EXPONENTIALITY | REMARKS |
|---|---|---|---|
| n > 8 and n < 25 |
|
|
|
| n > 25 and n < 125 |
|
| Chi-Square Goodness-of-Fit test
|
| n >125 |
|
|
|
| Not recommended: (1) Kolmogorow-Smirnov (2) Standard Chi-Square Goodness-of-Fit test over pretabulated data | |||
|