Six Sigma and Beyond: Design for Six Sigma, Volume VI
In Chapter 11, we discussed axiomatic design and its four mapping domains (CAs, FRs, DPs, and PVs). Now, let us examine some of the mathematical relations for these domains. If, for example, we are interested in the functional requirements [FR(CTS)], then this can be expressed in the traditional six sigma notation of y = f(x) as FR = f( DP ), where DP (design parameter) is an array of the mapped to DPs of size m. If we let each DP in the array be written as DP i = g(PV i ), where PV i , i = 1,...,m, is an array of process variables that the mapped to DP i , soft changes may be implemented using sensitivities in physical (FR and DP) and process (DP and PV) mapping. Using the chain rule, we have:
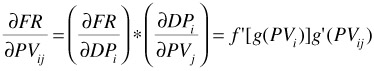
where PV ij is a process variable in the array PV j that can be adjusted to improve the problematic FR. The first term represents a design change while the second one represents a process change. An efficient DFSS strategy should utilize both terms in all potential improvements. After all, the ideal DFSS outcome is a design that a) exceeds customer wants, needs and expectations, b) exceeds competition market performance as measured by reliability, robustness, and life cycle costs indices, and c) the rest of product features.
This is very important because as we said earlier, DFSS is not for all designs and processes. We must be selective in how we use it. Table 14.1 may be of help.
| Z s | Z s does not exist | Z s exists |
|---|---|---|
| X s does not exist | No problem; this type of design may not exist | Need conceptual change; DFSS has potential while six sigma has no potential |
| X s exists | Trivial problem; this type may be solved with design of experiments (DOE) | Both six sigma and DFSS have potential |
A final point about the axiomatic designs. The importance of the design or problem matrix has many perspectives. The main one is the revealing of coupling among the CTs. Knowledge of coupling is important because it gives the designer clues about where to find solutions, and make adjustments or changes and how to maintain them over the long term with minimal drift .
So, for the uncoupled matrix we have

For the coupled matrix we have
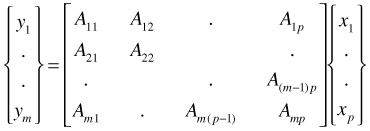
For the decoupled matrix we have
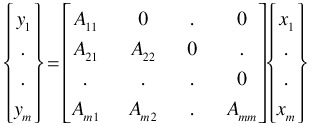
These design matrices are obtained in a hierarchy when the zigzagging method is used (see Chapter 11). At lower levels of hierarchy, sensitivities can be obtained mathematically as the CTSs take the form of basic physical and engineering quantities . In some cases they are not available, and that means that the experimenter has to rely on some kind of simulation or modeling.