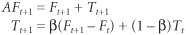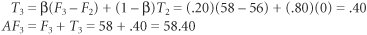Introduction to Management Science (10th Edition)

[Page 703]

The following problem provides an example of the computation of exponentially smoothed and adjusted exponentially smoothed forecasts.

Problem Statement

A computer software firm has experienced the following demand for its Personal Finance software package:

Period

Units

1

56

2

61

3

55

4

70

5

66

6

65

7

72

8

75

Develop an exponential smoothing forecast, using a = .40, and an adjusted exponential smoothing forecast, using a = .40 and b = .20. Compare the accuracy of the two forecasts, using MAD and cumulative error.

Solution

Step  1.

Compute the Exponential Smoothing Forecast

F t +1 = a D t + (1 a ) F t

For period 2 the forecast ( assuming that F 1 = 56) is

F 2 = a D 1 + (1 a ) F 1 = (.40)(56) + (.60)(56) = 56

For period 3 the forecast is

F 3 = (.40)(61) + (.60)(56) = 58

The remaining forecasts are computed similarly and are shown in the table on page 704.

Step  2.

Compute the Adjusted Exponential Smoothing Forecast

Starting with the forecast for period 3 (because F 1 = F 2 and we will assume that T 2 = 0),

[Page 704]
The remaining adjusted forecasts are computed similarly and are shown in the following table:

Period

D t

F t

AF t

D t F t

D t AF t

1

56

2

61

56.00

56.00

5.00

5.00

3

55

58.00

58.40

3.00

3.40

4

70

56.80

56.88

13.20

13.12

5

66

62.08

63.20

3.92

2.80

6

65

63.65

64.86

1.35

0.14

7

72

64.18

65.26

7.81

6.73

8

75

67.31

68.80

7.68

6.20

9

70.39

72.19

       

35.97

30.60

Step  3.

Compute the MAD Values

Step  4.

Compute the Cumulative Error

Because both MAD and the cumulative error are less for the adjusted forecast, it would appear to be the most accurate.

The following problem provides an example of the computation of a linear regression forecast.

Problem Statement

A local building products store has accumulated sales data for two-by-four lumber (in board feet) and the number of building permits in its area for the past 10 quarters :

Quarter

Building Permits, x

Lumber Sales (1,000s of bd. ft.), y

1

8

12.6

2

12

16.3

3

7

9.3

4

9

11.5

5

15

18.1

6

6

7.6

7

5

6.2

8

8

14.2

9

10

15.0

10

12

17.8

[Page 705]

Develop a linear regression model for these data and determine the strength of the linear relationship by using correlation. If the model appears to be relatively strong, determine the forecast for lumber, given 10 building permits in the next quarter.

Solution

Step  1.

Compute the Components of the Linear Regression Equation

Step  2.

Develop the Linear Regression Equation

y = a + bx

y = 1.36 + 1.25 x

Step  3.

Compute the Correlation Coefficient

Thus, there appears to be a strong linear relationship.

Step  4.

Calculate the Forecast for x = 10 Permits

Related

Категории